دنباله اعداد کاتالان

دنباله اعداد کاتالان (Catalan Numbers) یکی از دنباله‌های عددی مشهور ریاضیات است که برای عدد نامنفی n به صورت C_n نمایش داده می‌شود.

C_n:    1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, ...

این دنباله کاربردهای بسیاری در مسائل شمارشی دارد. از جمله:

دنباله اعداد کاتالان (Catalan Numbers) یکی از دنباله‌های عددی مشهور ریاضیات است که برای عدد نامنفی n به صورت C_n نمایش داده می‌شود.

C_n:    1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, ...

این دنباله کاربردهای بسیاری در مسائل شمارشی دارد. از جمله:

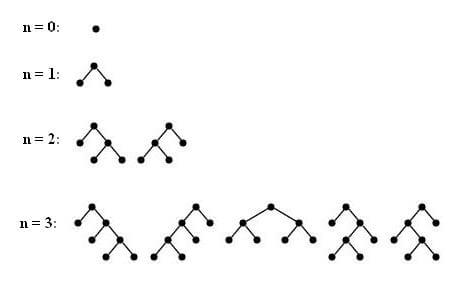
1- تعداد درخت‌های دودویی با n راس داخلی برابر C_n است:

                                   

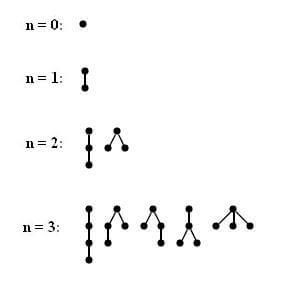
2- تعداد درخت‌ها با n یال برابر C_n است:  

                             

 3- تعداد پرانتزبندی‌های صحیح با استفاده از n جفت پرانتز باز و بسته برابر C_n است: 

n = 0:	*	1 way
n = 1:	()	1 way
n = 2:	()(), (())	2 ways
n = 3:	()()(), ()(()), (())(), (()()), ((()))	5 ways
n = 4:	()()()(), ()()(()), ()(())(), ()(()()), ()((())),                                           (())()(), (())(()), (()())(), ((()))(), (()()()), (()(())), ((())()), ((()())), (((())))	14 ways
n = 5:	()()()()(), ()()()(()), ()()(())(), ()()(()()), ()()((())),                              ()(())()(), ()(())(()), ()(()())(), ()((()))(), ()(()()()), ()(()(())), ()((())()), ()((()())), ()(((()))), (())()()(), (())()(()), (())(())(), (())(()()), (())((())), (()())()(), (()())(()), ((()))()(), ((()))(()), (()()())(), (()(()))(), ((())())(), ((()()))(), (((())))(), (()()()()), (()()(())), (()(())()), (()(()())), (()((()))), ((())()()), ((())(())), ((()())()), (((()))()), ((()()())), ((()(()))), (((())())),(((()()))), ((((()))))	42 ways

4- تعداد پرانتزبندی‌های صحیح n عبارت ریاضی برابر C_n-1 است:

( A )	n = 1
( A B )	n = 2
( ( A B ) C )    ,    ( A ( B C ) )	n = 3
( ( ( A B ) C ) D )    ,    ( ( A ( B C ) ) D )    ,    ( ( A B ) ( C D ) ) A ( ( B C ) D )    ,     ( A ( B ( C D ) ) )	n = 4

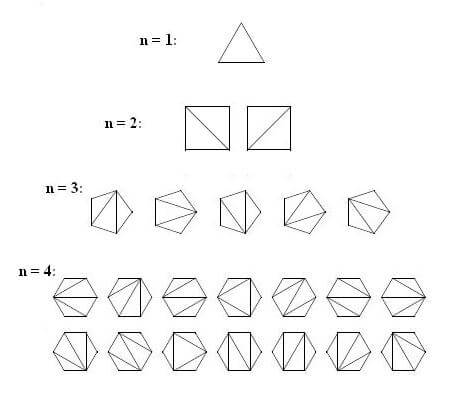
5- تعداد روش‌های مثلث‌بندی یک چندضلعی محدب با n + 2  ضلع برابر C_n است:

                                     

6- با بررسی تحلیلی این مسائل، رابطه بازگشتی زیر برای محاسبه جملات دنباله اعداد کاتالان به دست آمده است:

                                     

  این تعریف، مقدار جمله nام دنباله را به مقادیر تمام جملات قبلی وابسته می‌کند. به عنوان مثال: 

C₁ = C₀ * C₀ = 1 * 1 = 1

C₂ = C₀ * C₁ + C₁ * C₀ = 1 * 1 + 1 * 1 = 2

C₃ = C₀ * C₂ + C₁ * C₁ + C₂ * C₀ = 1 * 2 + 1 * 1 + 2 * 1 = 5

رابطه غیربازگشتی اعداد کاتالان

تا به این جا با تعریف بازگشتی دنباله کاتالان سر و کار داشتیم. اما این دنباله بازگشتی را می‌توان با استفاده از روابط ریاضی حل کرده، و به یک رابطه غیربازگشتی دست یافت.

حل تحلیلی دنباله کاتالان با استفاده از توابع مولد رابطه زیر را نتیجه می‌دهد 

                                                                           

 می‌توان رابطه بازگشتی زیر را نتیجه گرفت:

                               

مسأله: یک صفحه ی شطرنجی n×n در نظر بگیرید؛ می‌خواهیم با حرکت روی خطوط صفحه ی شطرنجی، از نقطه ی A در گوشه ی سمت چپ پائین صفحه، شروع کرده و به نقطه ی B در گوشه ی سمت راست بالای صفحه برسیم. شرط کار این است که فقط می‌توانیم به سمت‌های راست و بالا حرکت کنیم و هرگز نباید به بالای قطر AB برویم. به چند طریق می‌توان از A به B رسید؟